Multi-phase VSD and Park transformation IP-Core

• IP-cores for multi-phase VSD and Park transformation (six-phase and nine-phase versions implemented individually)

• Applies multi-phase VSD transformation to input and Park transformation to only alpha and beta values

• Performs respective inverse transformation

• Input interface is PL-only

• Transformation can only be triggered by a PL signal, but not by the software driver

• Output is supplied to PL-ports as well as AXI

• Inputs and outputs are fixed point

• The AXI values of theta_el_axi and x_abc_out_axi are updated to the current output whenever the input trigger_new_values is high, to allow synchronous sampling in combination with a PWM module

Table 112 Interface of Transformation IP-Core

Port Name	Port Type	Data Type	Interface	Range	Description	Six-phase	Nine-phase
theta_el	Input	sfix18_En14	External Signal	-8 to +7	electric rotor angle	y	y
theta_el_axi	Output	sfix18_En14	AXI 0x100	-8 to +7	electric rotor angle	y	y
trigger_new_values	Input	boolean	External Signal		trigger to update outputs	y	y
x_abc1_ll_pl	Input	sfix27_En16 (3)	External Signal	-1024 to +1023	input phase values subset 1 for transformation as line-to-line	y	y
x_abc2_ll_pl	Input	sfix27_En16 (3)	External Signal	-1024 to +1023	input phase values subset 2 for transformation as line-to-line	y	y
x_abc3_ll_pl	Input	sfix27_En16 (3)	External Signal	-1024 to +1023	input phase values subset 3 for transformation as line-to-line	n	y
x_out_dq	Output	sfix27_En16 (6/9)	External Signal	-1024 to +1023	output transfomed values	y	y
x_in_dq	Input	sfix27_En18 (6/9)	External Signal	-256 to +255	input dq values for inverse transformation	y	y
x_abc_out_axi	Output	sfix27_En18 (6/9)	AXI 0x140	-256 to +255	output inverse transformed abc values to AXI	y	y
x_abc_1	Output	sfix27_En18 (3)	External Signal	-256 to +255	output inverse transformed abc subset 1 values	y	y
x_abc_2	Output	sfix27_En18 (3)	External Signal	-256 to +255	output inverse transformed abc subset 2 values	y	y
x_abc_3	Output	sfix27_En18 (3)	External Signal	-256 to +255	output inverse transformed abc subset 3 values	n	y
refresh_values	Output	boolean	External Signal		feedback signal that trigger_new_values input has been acknowledged and outputs are updated	y	y

VSD and Park transformation

The IP-Core applies the transformations to the inputs x_abc1_ll_pl, x_abc2_ll_pl (and x_abc3_ll_pl for nine-phase IP-core). The values must be supplied as line-to-line values because a transformation to star values is applied in the IP-Core before applying the VSD transformation. The line-to-line to star-value transformation is realized by applying the Clarke transformation to each three-phase subset, dividing the amplitudes by \(\sqrt{3}\) and rotating the pointers by -30° before applying the inverse Clarke transformation. Although the naming “x” suggests, any values can be used as input, the intention is to use line-to-line voltages as input. After the transformation to the stationary reference frame by application of the VSD transformation, the Park transformation is applied to the alpha and beta values only, yielding the following output vector (see below). Note that the min and max values of the output vector (defined by the fixed-point datatype) are significantly smaller than the ones of the input values and must be taken into account when using the IP-core.

Six-phase transformation

\[\textrm{x_out_dq}= \begin{bmatrix} x_{d} & x_{q} & x_{x} & x_{y} & x_{z1} & x_{z2} \end{bmatrix} ^T\]

The IP-core uses the following VSD matrix according to [[1]] to transform the phase variables to the stationary reference frame:

\[\begin{split}\begin{bmatrix} C \end{bmatrix}= \frac{1}{3} \begin{bmatrix} cos(1\cdot 0\cdot\frac{\pi}{6}) & cos(1\cdot 4\cdot\frac{\pi}{6}) & cos(1\cdot 8\cdot\frac{\pi}{6}) & cos(1\cdot 1\cdot\frac{\pi}{6}) & cos(1\cdot 5\cdot\frac{\pi}{6}) & cos(1\cdot 9\cdot\frac{\pi}{6}) \\ sin(1\cdot 0\cdot\frac{\pi}{6}) & sin(1\cdot 4\cdot\frac{\pi}{6}) & sin(1\cdot 8\cdot\frac{\pi}{6}) & sin(1\cdot 1\cdot\frac{\pi}{6}) & sin(1\cdot 5\cdot\frac{\pi}{6}) & sin(1\cdot 9\cdot\frac{\pi}{6}) \\ cos(5\cdot 0\cdot\frac{\pi}{6}) & cos(5\cdot 4\cdot\frac{\pi}{6}) & cos(5\cdot 8\cdot\frac{\pi}{6}) & cos(5\cdot 1\cdot\frac{\pi}{6}) & cos(5\cdot 5\cdot\frac{\pi}{6}) & cos(5\cdot 9\cdot\frac{\pi}{6}) \\ sin(5\cdot 0\cdot\frac{\pi}{6}) & sin(5\cdot 4\cdot\frac{\pi}{6}) & sin(5\cdot 8\cdot\frac{\pi}{6}) & sin(5\cdot 1\cdot\frac{\pi}{6}) & sin(5\cdot 5\cdot\frac{\pi}{6}) & sin(5\cdot 9\cdot\frac{\pi}{6}) \\ cos(3\cdot 0\cdot\frac{\pi}{6}) & cos(3\cdot 4\cdot\frac{\pi}{6}) & cos(3\cdot 8\cdot\frac{\pi}{6}) & cos(3\cdot 1\cdot\frac{\pi}{6}) & cos(3\cdot 5\cdot\frac{\pi}{6}) & cos(3\cdot 9\cdot\frac{\pi}{6}) \\ sin(3\cdot 0\cdot\frac{\pi}{6}) & sin(3\cdot 4\cdot\frac{\pi}{6}) & sin(3\cdot 8\cdot\frac{\pi}{6}) & sin(3\cdot 1\cdot\frac{\pi}{6}) & sin(3\cdot 5\cdot\frac{\pi}{6}) & sin(3\cdot 9\cdot\frac{\pi}{6}) \\ \end{bmatrix}\end{split}\]

Nine-phase transformation

\[\textrm{x_out_dq}= \begin{bmatrix} x_{d} & x_{q} & x_{x1} & x_{y1} & x_{x2} & x_{y2} & x_{x3} & x_{y3} & x_{zero} \end{bmatrix} ^T\]

The IP-core uses the following VSD matrix according to [[2]][[3]] to transform the phase variables to the stationary reference frame:

\[\begin{split}\begin{bmatrix} C \end{bmatrix}= \frac{2}{9} \begin{bmatrix} cos(1\cdot 0\cdot\frac{\pi}{9}) & cos(1\cdot 6\cdot\frac{\pi}{9}) & cos(1\cdot 12\cdot\frac{\pi}{9}) & cos(1\cdot 1\cdot\frac{\pi}{9}) & cos(1\cdot 7\cdot\frac{\pi}{9}) & cos(1\cdot 13\cdot\frac{\pi}{9}) & cos(1\cdot 2\cdot\frac{\pi}{9}) & cos(1\cdot 8\cdot\frac{\pi}{9}) & cos(1\cdot 14\cdot\frac{\pi}{9}) &\\ sin(1\cdot 0\cdot\frac{\pi}{9}) & sin(1\cdot 6\cdot\frac{\pi}{9}) & sin(1\cdot 12\cdot\frac{\pi}{9}) & sin(1\cdot 1\cdot\frac{\pi}{9}) & sin(1\cdot 7\cdot\frac{\pi}{9}) & sin(1\cdot 13\cdot\frac{\pi}{9}) & sin(1\cdot 2\cdot\frac{\pi}{9}) & sin(1\cdot 8\cdot\frac{\pi}{9}) & sin(1\cdot 14\cdot\frac{\pi}{9}) \\ cos(3\cdot 0\cdot\frac{\pi}{9}) & cos(3\cdot 6\cdot\frac{\pi}{9}) & cos(3\cdot 12\cdot\frac{\pi}{9}) & cos(3\cdot 1\cdot\frac{\pi}{9}) & cos(3\cdot 7\cdot\frac{\pi}{9}) & cos(3\cdot 13\cdot\frac{\pi}{9}) & cos(3\cdot 2\cdot\frac{\pi}{9}) & cos(3\cdot 8\cdot\frac{\pi}{9}) & cos(3\cdot 14\cdot\frac{\pi}{9}) \\ sin(3\cdot 0\cdot\frac{\pi}{9}) & sin(3\cdot 6\cdot\frac{\pi}{9}) & sin(3\cdot 12\cdot\frac{\pi}{9}) & sin(3\cdot 1\cdot\frac{\pi}{9}) & sin(3\cdot 7\cdot\frac{\pi}{9}) & sin(3\cdot 13\cdot\frac{\pi}{9}) & sin(3\cdot 2\cdot\frac{\pi}{9}) & sin(3\cdot 8\cdot\frac{\pi}{9}) & sin(3\cdot 14\cdot\frac{\pi}{9}) \\ cos(5\cdot 0\cdot\frac{\pi}{9}) & cos(5\cdot 6\cdot\frac{\pi}{9}) & cos(5\cdot 12\cdot\frac{\pi}{9}) & cos(5\cdot 1\cdot\frac{\pi}{9}) & cos(5\cdot 7\cdot\frac{\pi}{9}) & cos(5\cdot 13\cdot\frac{\pi}{9}) & cos(5\cdot 2\cdot\frac{\pi}{9}) & cos(5\cdot 8\cdot\frac{\pi}{9}) & cos(5\cdot 14\cdot\frac{\pi}{9}) \\ sin(5\cdot 0\cdot\frac{\pi}{9}) & sin(5\cdot 6\cdot\frac{\pi}{9}) & sin(5\cdot 12\cdot\frac{\pi}{9}) & sin(5\cdot 1\cdot\frac{\pi}{9}) & sin(5\cdot 7\cdot\frac{\pi}{9}) & sin(5\cdot 13\cdot\frac{\pi}{9}) & sin(5\cdot 2\cdot\frac{\pi}{9}) & sin(5\cdot 8\cdot\frac{\pi}{9}) & sin(5\cdot 14\cdot\frac{\pi}{9}) \\ cos(7\cdot 0\cdot\frac{\pi}{9}) & cos(7\cdot 6\cdot\frac{\pi}{9}) & cos(7\cdot 12\cdot\frac{\pi}{9}) & cos(7\cdot 1\cdot\frac{\pi}{9}) & cos(7\cdot 7\cdot\frac{\pi}{9}) & cos(7\cdot 13\cdot\frac{\pi}{9}) & cos(7\cdot 2\cdot\frac{\pi}{9}) & cos(7\cdot 8\cdot\frac{\pi}{9}) & cos(7\cdot 14\cdot\frac{\pi}{9}) \\ sin(7\cdot 0\cdot\frac{\pi}{9}) & sin(7\cdot 6\cdot\frac{\pi}{9}) & sin(7\cdot 12\cdot\frac{\pi}{9}) & sin(7\cdot 1\cdot\frac{\pi}{9}) & sin(7\cdot 7\cdot\frac{\pi}{9}) & sin(7\cdot 13\cdot\frac{\pi}{9}) & sin(7\cdot 2\cdot\frac{\pi}{9}) & sin(7\cdot 8\cdot\frac{\pi}{9}) & sin(7\cdot 14\cdot\frac{\pi}{9}) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \end{bmatrix}\end{split}\]

Inverse VSD and Park transformation

The input x_in_dq is used for the inverse transformation. The d and q values are transformed to alpha and beta with the inverse Park transformation. Afterward, the inverse VSD transformation is applied which yields the phase variables. The phase variables are output as star values and not line-to-line values!

Driver reference

Six-phase transformation

typedef struct uz_pmsm6ph_transformation_t uz_pmsm6ph_transformation_t

struct uz_pmsm6ph_config_t

Configuration struct for the PMSM model IP-Core driver.

uz_pmsm6ph_transformation_t *uz_pmsm6ph_transformation_init(struct uz_pmsm6ph_config_t config)

Initialize an instance of the driver.

Parameters:

• config – Config struct

Returns:

uz_pmsm6ph_transformation_t* Pointer to an initialized instance of the driver

uz_6ph_abc_t uz_pmsm6ph_transformation_get_currents(uz_pmsm6ph_transformation_t *self)

Returns the results of the inverse transformation (phase varivables)

Parameters:

• self – Pointer to driver instance

Returns:

struct uz_6ph_abc_t Output values

float uz_pmsm6ph_transformation_get_theta_el(uz_pmsm6ph_transformation_t *self)

Returns theta electric.

Parameters:

• self – Pointer to driver instance

Returns:

float theta electric

Nine-phase transformation

typedef struct uz_pmsm9ph_transformation_t uz_pmsm9ph_transformation_t

struct uz_pmsm9ph_config_t

Configuration struct for the PMSM model IP-Core driver.

uz_pmsm9ph_transformation_t *uz_pmsm9ph_transformation_init(struct uz_pmsm9ph_config_t config)

Initialize an instance of the driver.

Parameters:

• config – Config struct

Returns:

uz_pmsm9ph_transformation_t* Pointer to an initialized instance of the driver

uz_9ph_abc_t uz_pmsm9ph_transformation_get_currents(uz_pmsm9ph_transformation_t *self)

Returns the results of the inverse transformation (phase varivables)

Parameters:

• self – Pointer to driver instance

Returns:

struct uz_9ph_abc_t Output values

float uz_pmsm9ph_transformation_get_theta_el(uz_pmsm9ph_transformation_t *self)

Returns theta electric.

Parameters:

• self – Pointer to driver instance

Returns:

float theta electric

Standalone use

Vivado

A small example of usage for the IP-core is given below. Note that the intended usage is in combination with the other CIL IP-core’s and this IP-core has not been optimized for standalone usage. To use this IP-core correctly, the RS Flip Flop needs to be added as well, as shown in the screenshot below.

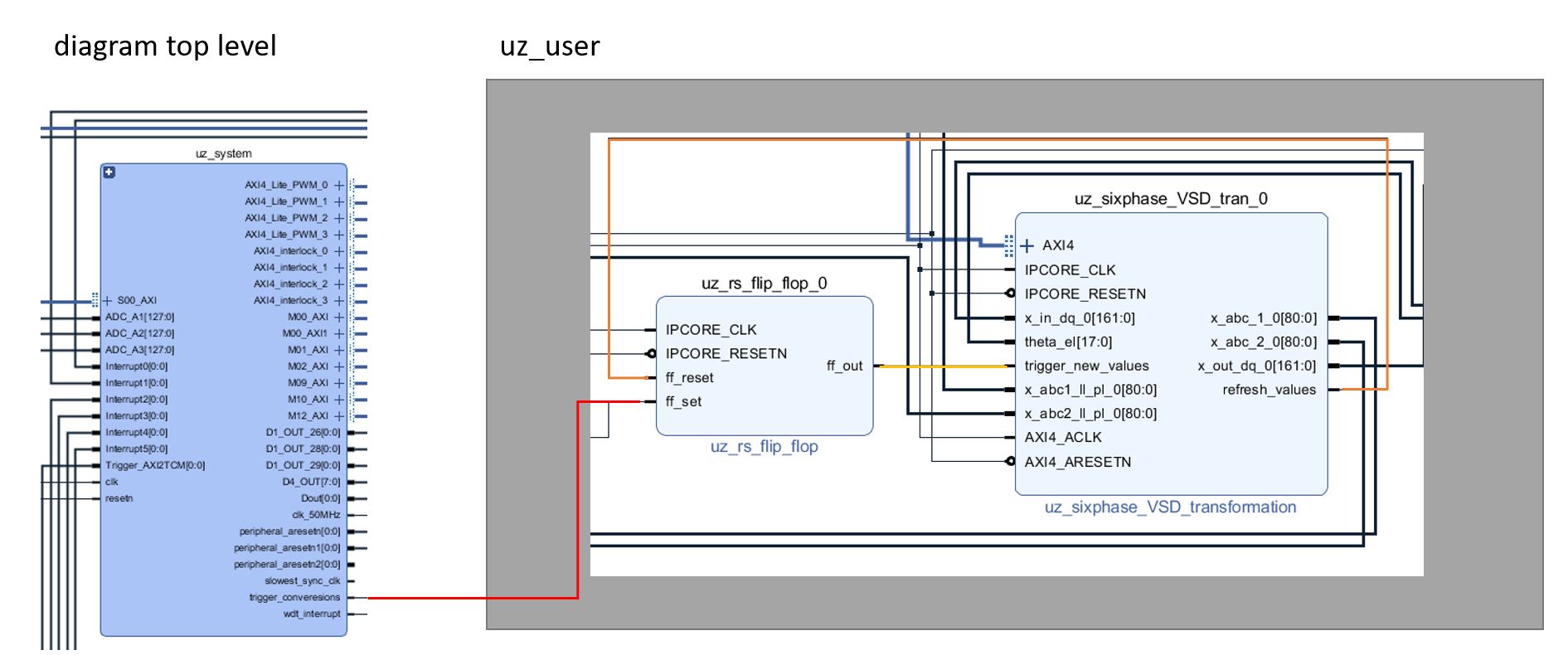
Fig. 349 Connection with Flip Flop

While most Ports of the IP-core should be used for the general application (as shown in CIL PMSM), special attention has to be paid to the trigger_new_values and refresh_values ports. The first of the two makes the IP-core give its current values to the PS and should be triggered by the trigger_conversions signal of the uz_system block, as it would be done for real ADC readouts. Since there are frequency differences in all those signals, it could be observed, that in some cases the trigger_conversions signal’s high time is too short to be detected by the IP-core (compare the following two figures).

Fig. 350 Correct timing for trigger signal (IP-core works)

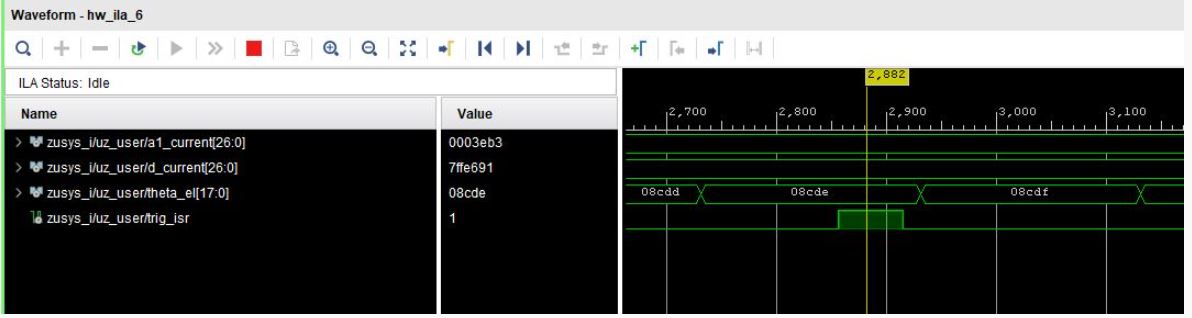
Fig. 351 Incorrect timing for trigger signal (outputs are never updated)

To synchronize the different clock domains used, the RS Flip Flop is placed, as shown in the first picture. The flip-flop is set by the trigger_conversions signal and as soon as the IP-core receives the high signal, it outputs an acknowledgment at the refresh_values port, which can be used to reset the flip-flop again.

Vitis

The following function calls show the minimal usage of this IP-core. Using it in combination with the whole CIL setup is shown in the example pages in more detail.

Listing 196 Changes in main.c (R5)

...
#include "IP_Cores/uz_pmsm6ph_transformation/uz_pmsm6ph_transformation.h"
uz_pmsm6ph_transformation_t* transformation = NULL;                           //pointer to transformation object
struct uz_pmsm6ph_config_t transformation_config = {                          //config to init transformation object
  .base_address = XPAR_UZ_USER_UZ_SIXPHASE_VSD_TRAN_0_BASEADDR,
   .ip_core_frequency_Hz = 100000000.0f
};
...
int main(void)
{
  ...
  case init_ip_cores:
    transformation = uz_pmsm6ph_transformation_init(transformation_config);   //init transformation object
  ...

Listing 197 Changes in isr.c (R5)

...
#include "../IP_Cores/uz_pmsm6ph_transformation/uz_pmsm6ph_transformation.h"
extern uz_pmsm6ph_transformation_t* transformation;                           //pointer to transformation object
uz_6ph_abc_t abc_currents = {0};                                              //variable to save currents
float theta_el = 0.0f;                                                        //variable to save theta_el
...
void ISR_Control(void *data)
{
  ...
  abc_currents = uz_pmsm6ph_transformation_get_currents(transformation);     //readout currents
  theta_el = uz_pmsm6ph_transformation_get_theta_el(transformation);         //readout theta_el
  ...

Verification

The following setup is used to test the IP-core’s functionality (example for nine-phase IP-core). It is not recommended to copy this setup, instead, the above explanation should be used.

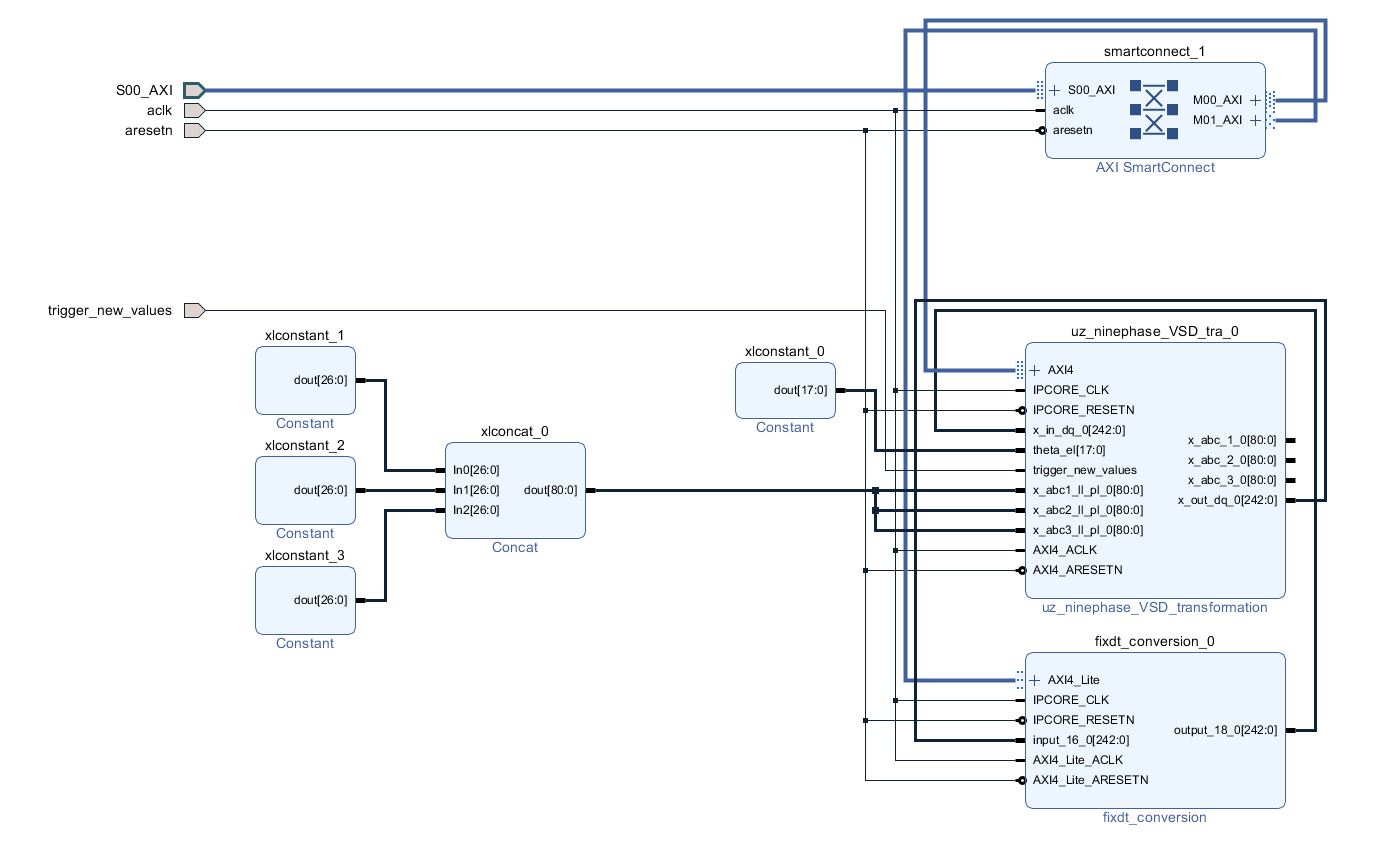
Fig. 352 Test setup for IP-core in Vivado

To test the IP-core, random values have been selected for the inputs (values are the same for all three subsets):

Table 113 Test values for IP-core

Port Name	Value Decimal	Value Hex
theta_el	\(\frac{\pi}{8}\)	0x1921
x_abc1/2/3_ll_pl(1)	111.9	0x06fe666
x_abc1/2/3_ll_pl(2)	31.55	0x01f8ccc
x_abc1/2/3_ll_pl(3)	-101.99	0x79a028f

The transformed output values from x_out_dq are fed back to the input x_in_dq. Because of the different fixed point datatypes of the port, a special datatype transformation IP-core was created, which is also present as an out-commented subsystem in the Simulink model of the main IP-core. The values of the inverse transformation are read out in the PS and are similar to the input values, after applying the line-to-line to star conversion to them. The output values from UZ and Simulink match and are shown in the following table.

Table 114 Test results for IP-core

Port Name	Value Decimal
theta_el_axi	0.3926392
x_abc_out_axi(1;4;7)	71.29803
x_abc_out_axi(2;5;8)	-26.78451
x_abc_out_axi(3;6;9)	-44.51395

Sources

[1]

8. Eldeeb, “Modelling, Control and Post-Fault Operation of Dual Three-phase Drives for Airborne Wind Energy,” Dissertation, Munich School of Engineering, 2019. [Online]. Available: https://mediatum.ub.tum.de/doc/1464393/1464393.pdf

[2]

1. 1. Rockhill and T. A. Lipo, “A generalized transformation methodology for polyphase electric machines and networks,” 2015 IEEE International Electric Machines & Drives Conference (IEMDC), 2015, pp. 27-34, doi: 10.1109/IEMDC.2015.7409032.

[3]

1. 1. Rockhill and T. A. Lipo, “A simplified model of a nine phase synchronous machine using vector space decomposition,” 2009 IEEE Power Electronics and Machines in Wind Applications, 2009, pp. 1-5, doi: 10.1109/PEMWA.2009.5208335.