Space vector limitation#

uz_3ph_dq_t uz_CurrentControl_SpaceVector_Limitation(uz_3ph_dq_t v_input_Volts, float V_dc_volts, float max_modulation_index, float omega_el_rad_per_sec, uz_3ph_dq_t i_ref_Ampere, bool *ext_clamping)#

function to limit reference voltages from a control algorithm of a 3ph-machine.

Parameters:

  • v_input_Volts – uz_3ph_dq_t struct with the voltages, which shall be limited

  • V_dc_volts – DC-link voltage

  • max_modulation_index – Max possible modulation index for the chosen modulation method. I.e. 1/sqrt(3) for Space-Vector-Modulation. Must be greater than 0.0f

  • omega_el_rad_per_sec – electrical rotational speed in rad/s

  • i_ref_Ampere – uz_3ph_dq_t struct for reference dq-currents in Ampere

  • ext_clamping – flag which states, if the SVL is active

Returns:

uz_3ph_dq_t

uz_6ph_dq_t uz_6ph_Space_Vector_Limitation(uz_6ph_dq_t v_input_Volts, float V_dc_volts, float max_modulation_index, float omega_el_rad_per_sec, uz_6ph_dq_t i_ref_Ampere, bool *ext_clamping)#

function to limit the voltages of a 6ph PMSM. Only applicable if the XY subspace is transformed with -theta_el and the 6ph-PMSM is in the 2N-configuration (separated neutral points).

Parameters:

  • v_input_Volts – uz_6ph_dq_t struct with the voltages, which shall be limited

  • V_dc_volts – DC-link voltage

  • max_modulation_index – Max possible modulation index for the chosen modulation method. I.e. 1/sqrt(3) for Space-Vector-Modulation. Must be greater than 0.0f

  • omega_el_rad_per_sec – electrical rotational speed in rad/s

  • i_ref_Ampere – uz_6ph_dq_t struct for reference dq-currents in Ampere

  • ext_clamping – flag which states, if the SVL is active

Returns:

uz_6ph_dq_t struct with limited voltages

Example#

Listing 147 Example function call for 3ph-space vector limitation#
 1#include "uz/uz_CurrentControl/uz_space_vector_limitation.h"
 2int main(void) {
 3   float V_dc_volts = 24.0f;
 4   float omega_el_rad_per_sec = 100.0f;
 5   uz_3ph_dq_t i_reference_Ampere = {.d = 1.0f, .q = 2.0f, .zero = 0.0f};
 6   uz_3ph_dq_t v_input_Volts = {.d = 5.0f, .q = 8.0f, .zero = 0.0f};
 7   bool ext_clamping = false;
 8   float max_modulation_index = 1.0f / sqrtf(3.0f);
 9   uz_3ph_dq_t output = uz_CurrentControl_SpaceVector_Limitation(v_input_Volts, V_dc_volts, max_modulation_index, omega_el_rad_per_sec, i_reference_Ampere, &ext_clamping);
10}
Listing 148 Example function call for 6ph-space vector limitation#
 1#include "uz/uz_CurrentControl/uz_space_vector_limitation.h"
 2int main(void) {
 3   float V_dc_volts = 24.0f;
 4   float omega_el_rad_per_sec = 100.0f;
 5   uz_6ph_dq_t i_reference_Ampere = {.d = 1.0f, .q = 2.0f, .x = 3.0f, y = 4.0f};
 6   uz_6ph_dq_t v_input_Volts = {.d = 5.0f, .q = 8.0f, .x = 10.0f, .y = 3.0f};
 7   bool ext_clamping = false;
 8   float max_modulation_index = 1.0f / sqrtf(3.0f);
 9   uz_6ph_dq_t output = uz_6ph_Space_Vector_Limitation(v_input_Volts, V_dc_volts, max_modulation_index, omega_el_rad_per_sec, i_reference_Ampere, &ext_clamping);
10}

Description#

Limitation for dq-axis#

Limits the input voltages according to the following flowchart. Further information can be found in [1] . This function is already included in the CurrentControl. With the max modulation index \(m_\mathrm{max}\) the following voltages can be calculated.

\[\begin{split}V_\mathrm{max} &= V_\mathrm{DC} \cdot m_\mathrm{max} \\ V_\mathrm{abs} &= \sqrt{v_d^2 + v_q^2}\end{split}\]

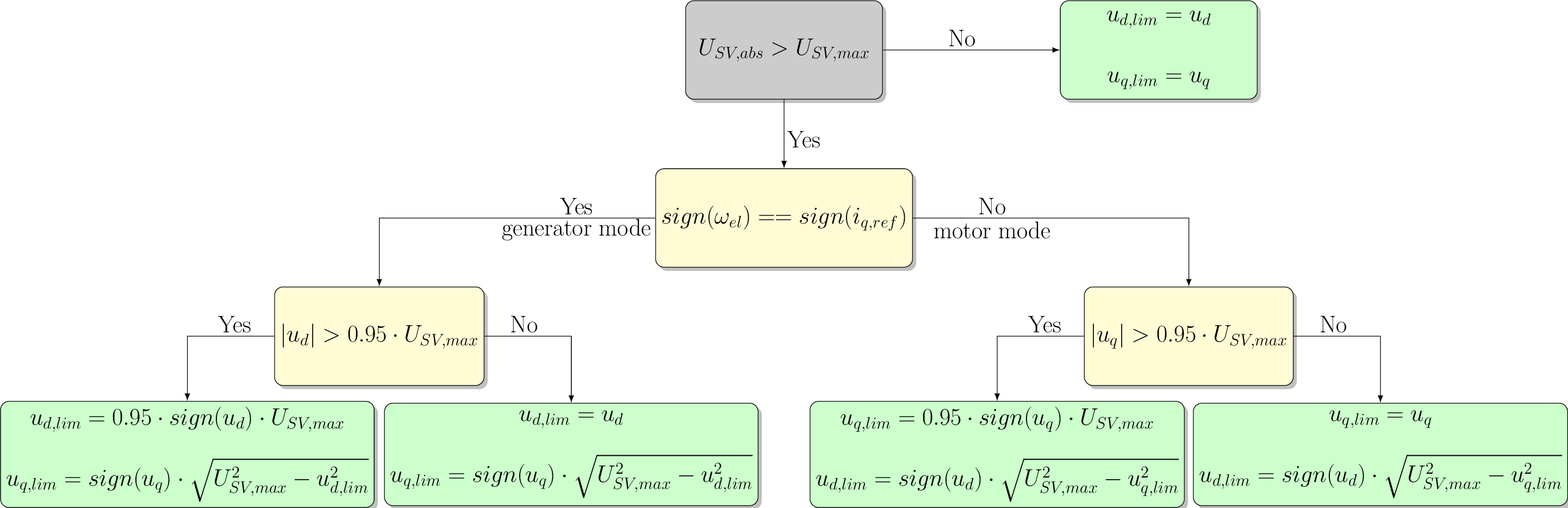
Figure made with TikZ

Fig. 298 space vector limitation flow chart for dq-axis

Limitation for six phases#

Limits the input voltages according to the following scheme.

Note

This only applies for a six-phase machine, where the \(\alpha\beta\)-system is transformed with \(\vartheta_{el}\) into the \(dq\) system and the \(XY\)-system is transformed with \(-\vartheta_{el}\) into the \(xy\)-system. The basis for the \(\alpha\beta\)- and \(XY\)-systems is the Coordinate Transformation. Furthermore, this approach is only valid, if the two neutral points of the 6ph-PMSM are disconnected from each other (2N-configuration).

With the max modulation index \(m_\mathrm{max}\), the maximum stator voltage according to

\[V_\mathrm{max} = V_\mathrm{DC} \cdot m_\mathrm{max}\,,\]

can be realized. First, the \(xy\)-subspace is limited to a maximum voltage of

\[V_\mathrm{lim}^{xy} = \frac{V_\mathrm{max}}{\sqrt{2}} = \frac{V_\mathrm{DC} \cdot m_{max}}{\sqrt{2}}\,.\]

The absolute value of the \(xy\)-voltages is

\[V_\mathrm{abs}^{xy} = \sqrt{v_x^2 + v_y^2}\,.\]

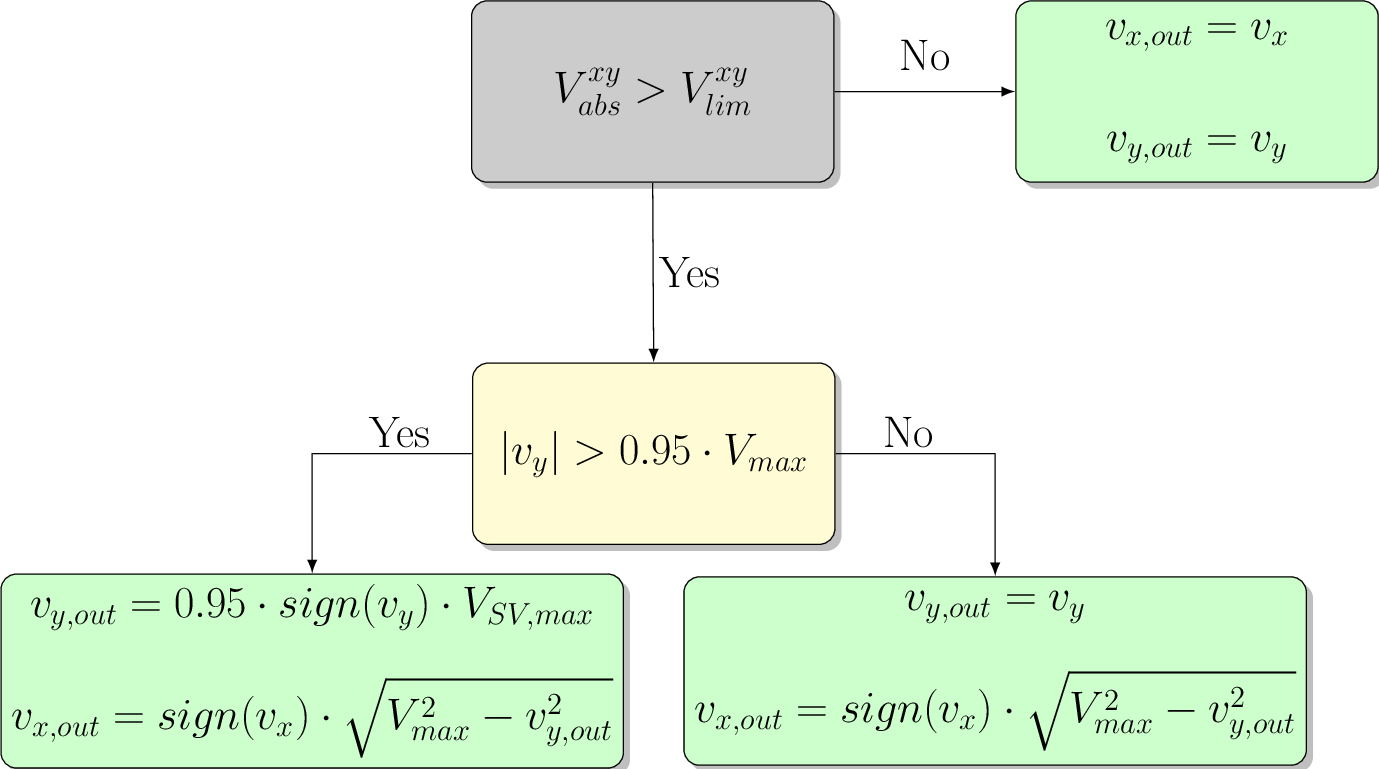
Figure made with TikZ

Fig. 299 space vector limitation flow chart for xy-axis

Afterwards, the \(dq\)-voltages are limited with the resulting voltages \(v_{x,out}\) and \(v_{y,out}\) of the \(xy\)-limitation according to

\[V_\mathrm{lim}^{dq} = \sqrt{V_\mathrm{max}^2 - (V_\mathrm{out}^{xy})^2}\,,\]

with

\[V_\mathrm{out}^{xy} = \sqrt{(v_\mathrm{out}^x)^2 + (v_\mathrm{out}^y)^2}\,,\]

being the limited voltages of the \(xy\)-axis which will be output.

The voltages of the \(dq\)-subspace are limited according to the flowchart in Fig. 298, with \(V_\mathrm{max}\) being replaced by \(V_\mathrm{lim}^{dq}\).

Sources#