Activation function#

The following activation functions are implemented.

Linear#

Figure made with TikZ

Activation function:

\[f(x)=x\]

Derivative:

\[f'(x)=1\]
float uz_nn_activation_function_linear(float x)#

Linear activation function, f(x)=x.

Parameters:

  • x –

Returns:

float

float uz_nn_activation_function_linear_derivative(float x)#

Derivative of linear activation function, f’(x)=1.

Parameters:

  • x –

Returns:

float

ReLU#

Rectified linear unit

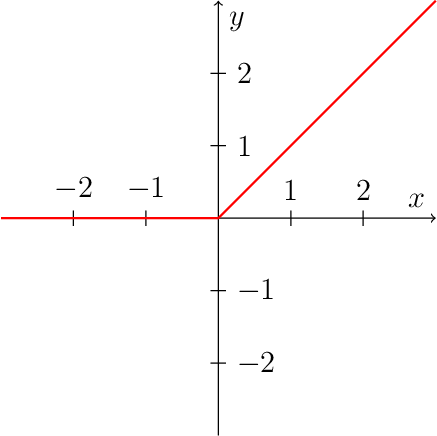
Figure made with TikZ

Activation function:

\[\begin{split}f(x) = \begin{cases} 0 & \text{if $x \leq 0$}\\ x & \text{if $x > 0$}\\ \end{cases}\end{split}\]

Derivative:

\[\begin{split}f'(x) = \begin{cases} 0 & \text{if $x \leq 0$}\\ 1 & \text{if $x > 0$}\\ \end{cases}\end{split}\]
float uz_nn_activation_function_relu(float x)#

Rectified linear unit, returns 0 if x <= 0, otherwise x.

Parameters:

  • x –

Returns:

float

float uz_nn_activation_function_relu_derivative(float x)#

Derivative of rectified linear unit, returns 0 if x <= 0, otherwise 1.0.

Parameters:

  • x –

Returns:

float

Leaky ReLU#

Leaky Rectified linear unit

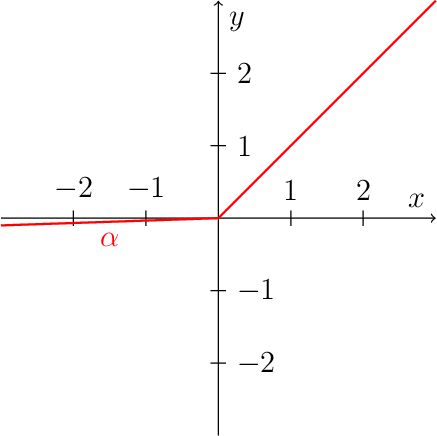
Figure made with TikZ

Activation function:

\[\begin{split}f(x) = \begin{cases} \alpha x & \text{if $x \leq 0$}\\ x & \text{if $x > 0$}\\ \end{cases}\end{split}\]

Derivative:

\[\begin{split}f'(x) = \begin{cases} \alpha & \text{if $x \leq 0$}\\ 1 & \text{if $x > 0$}\\ \end{cases}\end{split}\]
float uz_nn_activation_function_leaky_relu(float x, float alpha)#

Leaky rectified linear unit, returns alpha*x if x <=0, otherwise x.

Parameters:

  • x –

  • alpha – Linear factor for x if x < 0. alpha has to be 1>alpha>0

Returns:

float

float uz_nn_activation_function_leaky_relu_derivative(float x, float alpha)#

Derivative of leaky rectified linear unit, returns alpha if x <=0, otherwise 1.0.

Parameters:

  • x –

  • alpha – Linear factor for x if x < 0. alpha has to be 1>alpha>0

Returns:

float

Sigmoid logistic based on e-function#

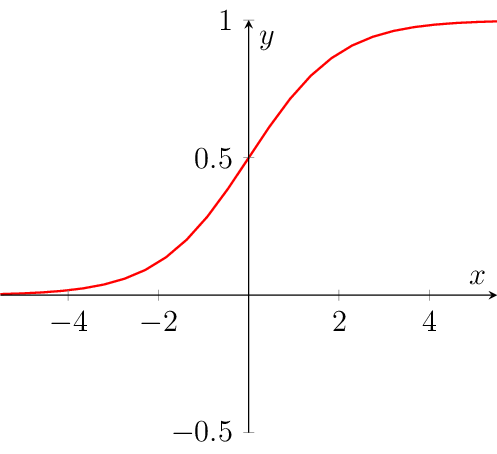
Figure made with TikZ

Calculates the logistic function (which is a special case of the sigmoid function). Calculation is based on the e-function.

Activation function ([1] page 76.):

\[f(x)=\frac{1}{1+e^{-x}}\]

Derivative ([1] page 76.):

\[f'(x)=f(x)(1-f(x))\]
float uz_nn_activation_function_sigmoid_logistic(float x)#

Calculates the sigmoid logistic function. Calculation based on e-function.

Parameters:

  • x –

Returns:

float

float uz_nn_activation_function_sigmoid_logistic_derivative(float x)#

Calculates the derivative of the sigmoid logistic function. Calculation based on e-function.

Parameters:

  • x –

Returns:

float

Sigmoid logistic based on tanh#

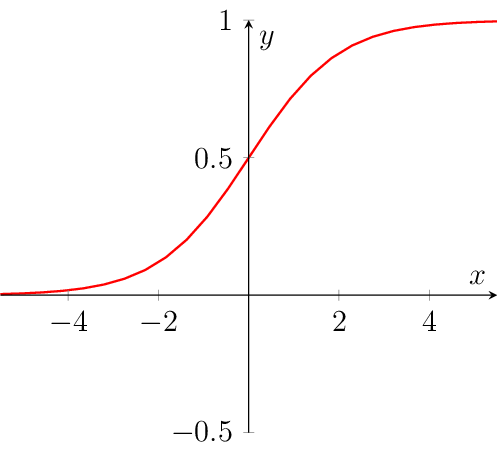
Figure made with TikZ

Calculates the logistic function (which is a special case of the sigmoid function). Calculation is based on the tanh-function.

Note

This function is slower than the version based on the e-function!

Activation function ([1] page 76.):

\[f(x)=0.5+0.5 \tanh(\frac{x}{2})\]

Derivative([1] page 76.):

\[f'(x)=f(x)(1-f(x))\]
float uz_nn_activation_function_sigmoid2_logistic(float x)#

Calculates the sigmoid logistic function. Calculation based on tanh.

Parameters:

  • x –

Returns:

float

float uz_nn_activation_function_sigmoid2_logistic_derivative(float x)#

Calculates the derivative of the sigmoid logistic function. Calculation based on tanh.

Parameters:

  • x –

Returns:

float

tanh#

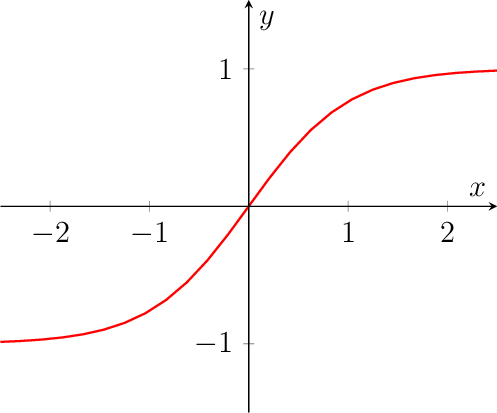
Figure made with TikZ

Calculates tanh activation function.

Activation ([1] page 76.):

\[f(x)=tanh(x)\]

Derivative ([1] page 76.):

\[f'(x)=1-f(x)^2\]
float uz_nn_activation_function_tanh(float x)#

Calculates tanh activation function.

Parameters:

  • x –

Returns:

float

float uz_nn_activation_function_tanh_derivative(float x)#

Calculates the derivative of tanh.

Parameters:

  • x –

Returns:

float

Sources#