Analog LTC2311-16 3v01

Diagrams

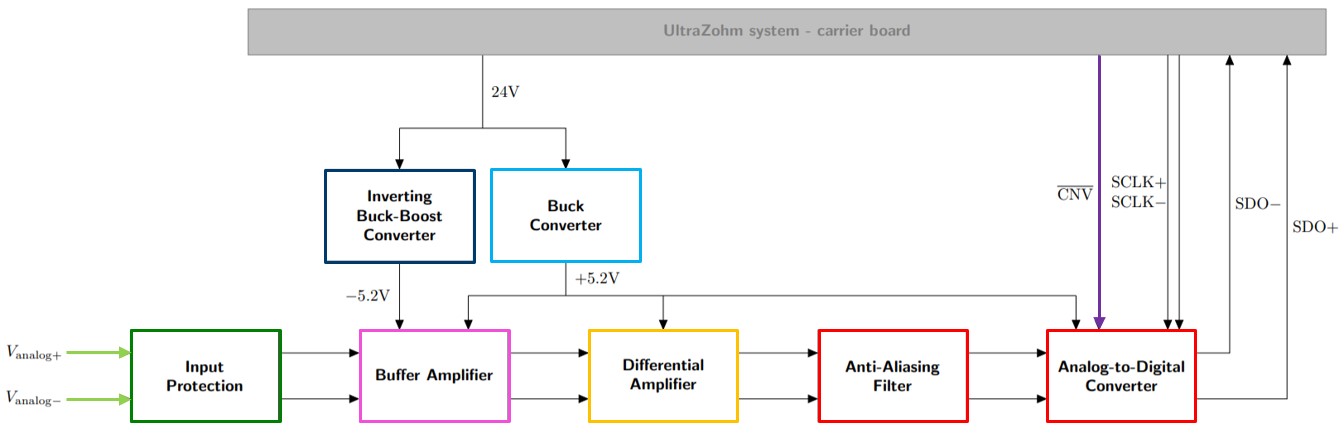
Block diagram

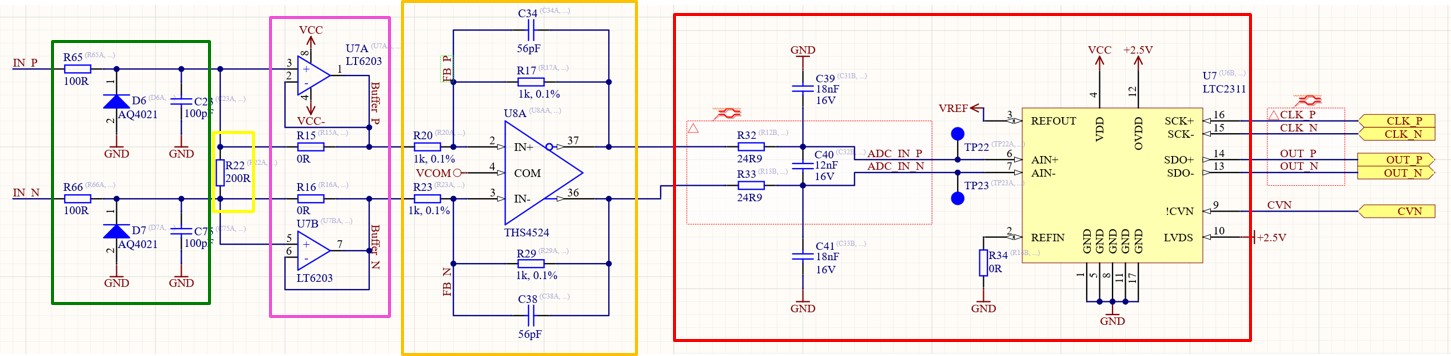
Schematic excerpt

PCB colored

From left to right

Notice that the picture of the PCB is flipped to match the orientation of the block diagram and schematic.

Color	Functionality
light green	Analog inputs on RJ45
dark green	Input protection (ESD diodes)
yellow	Measurement shunt resistor (optional, not populated)
pink	Voltage follower to increase input impedance and avoid loading the sensor
orange	Differential OpAmp to scale and filter signals
red	Anti-aliasing filter and ADC
dark blue	Inverting buck-boost converter for -5V
light blue	Buck converter for +5V
purple	Buffer for CNV signal coming from the FPGA

Filters

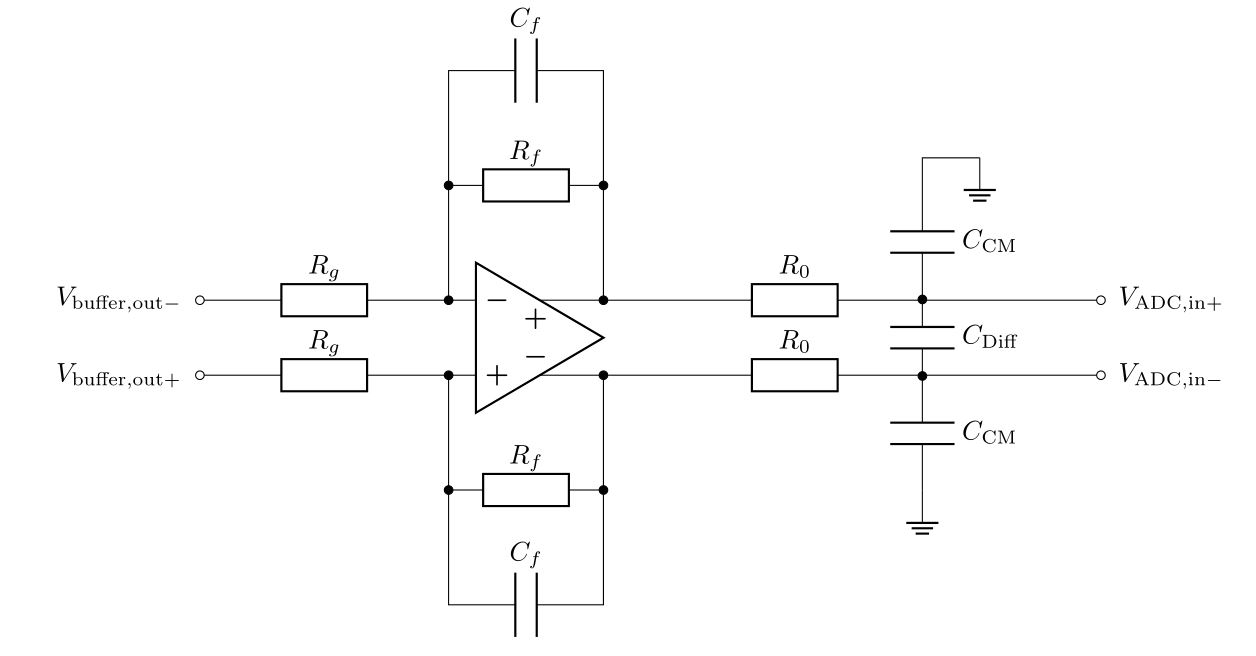
1. The crossover frequency \(f_\mathrm{aliasing,-3dB}\) of the anti-aliasing filter (red) is formed by the capacitors \(C_\mathrm{Diff}\) and \(C_\mathrm{CM}\). They create a first order low-pass filter with the series resistors \({R_0}\) with

\[f_\mathrm{aliasing,-3dB}=\frac{1}{2 \pi R_0 (2 C_\mathrm{Diff} + C_\mathrm{CM} ) } = \frac{1}{2\pi\ 24.9\,\Omega \cdot (2\cdot16\,\mathrm{nF} + 12\,\mathrm{nF}) } = 145\, \mathrm{kHz} \,\,.\]

2. Additionally, \(C_\mathrm{f}\) and \(R_\mathrm{f}\) form an active first-order low-pass filter, with

\[f_\mathrm{DiffOp,-3dB} = \frac{1}{2\pi R_f C_f} \approx \, 3 \mathrm{MHz}\]

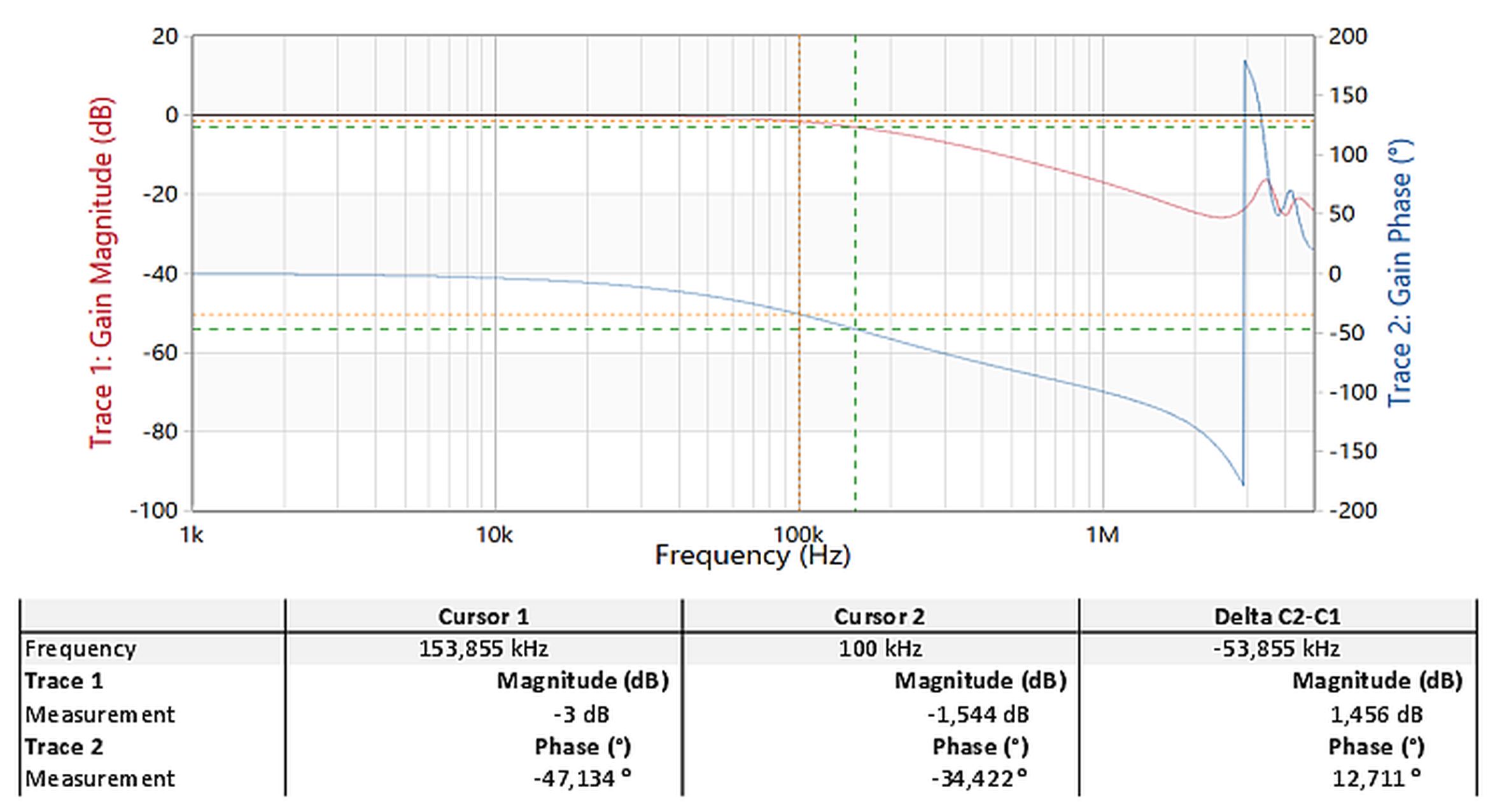
The resulting transfer function of the signal conditioning stage, i.e., from the RJ45 input connectors to the \(V_\mathrm{ADC,in}\) (including the buffer and filter stages up to the point where the signal enters the ADC), is measured with the Bode100. The resulting bode plot is depicted below.

Measurement accuracy

The signal conditioning stage of the adapter card is validated with a 6 1/2 digit multimeter yielding the following results. This suggests that a measurement error below 2mV can be expected over the full input range.

Adjust measurement gains

For all types of measurements, described in Measurement modes, it is recommended to adjust the gains of the differential operational amplifier (orange) to utilize the full input range of the ADC, i.e., \({\pm 5}\) V. Initially, the gain is set to

\[g=\frac{R_f}{R_g} = \frac{1\,\mathrm{k\Omega}}{1\,\mathrm{k\Omega}} = 1 \,\,.\]

Note

Use a high precision resistor to set the gains, i.e., 0.1% or better.

The pre-assembled values are

\({R_f}\)	\({1\,\mathrm{k\Omega}}\)
\({R_g}\)	\({1\,\mathrm{k\Omega}}\)
\({C_f}\)	\({56\,\mathrm{pF}}\)
\({R_0}\)	\({24.9\,\mathrm{\Omega}}\)
\({C_\mathrm{CM}}\)	\({12\,\mathrm{nF}}\)
\({C_\mathrm{Diff}}\)	\({16\,\mathrm{nF}}\)

Note

You can also use the LTSpice simulation to find the correct gains and filter values for your setup. The simulation files are attached at the end of this document.

Compatibility

• Slots A1 to A3 can be used without limitations

References

• Schematic 3v03

• Assembly Drawing 3v03

• LTSpice simulation

• See IP-Core ADC LTC2311

• Data sheet ADC LTC2311-16

Designed by

Simon Lukas (TUM), Eyke Liegmann (TUM) in 09/2020